
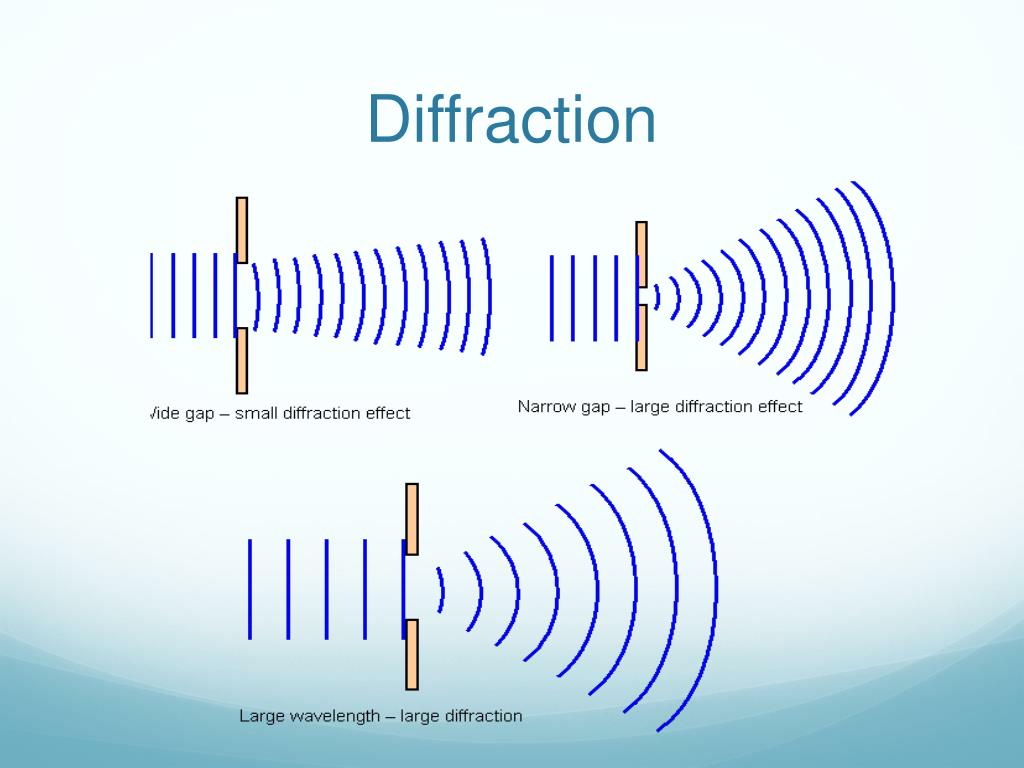
This is due to the addition, or interference, of different points on the wavefront (or, equivalently, each wavelet) that travel by paths of different lengths to the registering surface. The characteristic bending pattern is most pronounced when a wave from a coherent source (such as a laser) encounters a slit/aperture that is comparable in size to its wavelength, as shown in the inserted image. In classical physics, the diffraction phenomenon is described by the Huygens–Fresnel principle that treats each point in a propagating wavefront as a collection of individual spherical wavelets. Appendix.Infinitely many points (three shown) along length d project phase contributions from the wavefront, producing a continuously varying intensity θ on the registering plate.The Measurement of the Fields of Circular Apertures The Measurement of the Diffracted Fields of Apertures the Field of an Infinite Slit The Measurement of the Transmission Coeffi- cients of Apertures The Measurement of Fields Diffracted by Three- Dimensional Obstacles-Spheres and Ellipsoids The Diffracted Field of Two Parallel Conducting Cylinders when the Incident Electric Field Is Parallel to Their Axes The Measurement of the Diffracted Fields of Circular and Elliptic Cylinders when the Incident Electric Field Is Perpendicular to the Axis of the Cylinder The Measurement of the Diffracted Fields of Cylinders when the Incident Electric Field Is Parallel to the Axis of the Cylinder The Measurement of the Diffracted Fields of Obstacles The Measurement of the Scattered Field by a Time-Separation Method: Pulse Techniques The Measurement of the Scattered Field by a Frequency-Separation Method: the Doppler Effect The Measurement of the Scattered Field by a Partial-Reflection Method The Measurement of the Scattered Field by Separation in the Field: Rotationally Symmetrical Scatterers The Measurement of the Scattered Field by Separation at the Source

The Measurement of the Scattered Field by a Cancellation Method The Measurement of the Total Field: the Standing-Wave-Ratio Method Methods of Measuring the Back-Scattering Cross Section of Obstacles Scattering by Disks and Transmission Through Apertures of More General Shape Scattering of Waves That Are Not Plane Scattering by a Circular Disk Transmission Through a Circular Aperture Scattering by an Infinite Strip Transmission Through a Slit Theory of Scattering By a Disk or Strip and Transmission Through an Aperture Scattering by Cylindrical Mirrors and Slotted Cylinders Scattering from Thin Wires and Strips Reduction of Scattering by Reactive Loading Scattering by Parallel Circular Cylinders The Surface Current on Elliptic Cylinders General Studies of the Diffracted Fields of Noncircular Cylinders

Theory of Diffraction and Scattering by Obstacles of More General Shape Theory of Diffraction and Scattering by Spheres The Diffracted Field of Perfectly Conducting Circular Cylinders at High Frequencies ka Large The Back-Scattering Cross Section of Circular Cylinders-Conducting, Dielectric, and Absorbing The Total Scattering Cross Section of Circular Conducting Cylinders Asymptotic Formulas for the Surface Currents on Circular Cylinders with Large ka The Field in Terms of the Surface Current on the Obstacle The Surface Currents on Perfectly Conducting Circular Cylinders in Plane-Wave Fields: the Eigenfunction Expansions The Graphical Representation and Description of the Diffracted Field of a Perfectly Conducting Cylinder when the Magnetic Field is Parallel to the Axis: ka = 3.1
A General Description of the Diffracted Field of a Cylinder when the Electric Field is Parallel to the Axis: ka = 3.1 The Graphical Representation of the Diffracted Field of a Perfectly Conducting Cylinder when the Electric Field is Parallel to the Axis: ka = 3.1 Theory of Diffraction and Scattering by Circular Cylinders The Elements of a Practical Problem in Electromagnetic Scattering and Diffraction Statement of the Problem and Definition of Terms


 0 kommentar(er)
0 kommentar(er)
